2020-05-03

AtCoder ABC 165

AtCoder

ABCD4完で水色パフォでした。以下振り返り。

A - We Love Golf

問題のリンク

概要

要は $A$ 以上、 $B$ 以下の数に $K$ の倍数が含まれるか否か。

制約

$1 ≤ A ≤ B ≤ 1000$
$1 ≤ K ≤ 1000$

考察

面倒なので愚直に全探索

コード

K = int(input())
A, B = map(int, input().split())

for i in range(A, B+1):
    if i%K==0:
        print('OK')
        exit()

print('NG')

B - 1%

問題のリンク

概要

初年度に100円を預ける。年率1%の利子がつく時、 $X$ 以上になるのは何年後か。

制約

$101 ≤ X ≤ 10 ^{18}$

考察

最初、1年毎に端数切り捨てという条件を忘れて実装してしまってたけど、提出前に確認して気づけた。（本番慣れしてきた証拠と思いたい。）

コード

X = int(input())

cnt = 0
m = 100
while True:
    m *= 1.01
    m = int(m)
    cnt += 1
    if m>=X:
        break

print(cnt)

C - Many Requirements

問題のリンク

概要

文字にするとややこしいので省略。

制約

ながいので省略。ただ制約的に全探索でも間に合う感じ。

考察

問題文を始め読んだ際、日本語の意味が理解できず5分以上は考え込んでしまった。
理解してしまえば、そのまま全探索で行ける問題。
ただ初回の提出の際にcombinations_with_replacement(range(1, M+1), N)をcombinations_with_replacement(range( M+1), N)と書いてしまい、0を含めた数列で探索してしまった。（1WA）
C問題はBまでと比べると実装が少し重くなり始めるけど、こういう系はbit全探索系の問題を何度か解く事で慣れてきた気がする。

コード

from itertools import combinations_with_replacement

N, M, Q = map(int, input().split())
q = []
for _ in range(Q):
    q.append(list(map(int, input().split())))

ans = 0
for v in combinations_with_replacement(range(1, M+1), N):
    score = 0
    for i in range(Q):
        joken = q[i]
        if v[joken[1]-1] - v[joken[0]-1] == joken[2]:
            score += joken[3]
    ans = max(ans, score)
    #print(v, ': ', score)

print(ans)

D - Floor Function

問題のリンク

概要

$N$ 以下の非負整数 $x$ に対する $floor(Ax/B) -A × floor(x/B)$ の最大値

制約

$1 ≤ A ≤ 10 ^{6}$
$1 ≤ B ≤ 10 ^{12}$
$1 ≤ N ≤ 10 ^{12}$
入力は全て整数

考察

$floor(x/B)$ が0となる範囲内で、最大の $x$ を求める。要は $x=B-1$
ただ $x$ が指定の範囲を取れない場合もある。よってその時の条件を忘れないことが肝。( $x=N$ )

コード

from math import floor

A, B, N = map(int, input().split())

if N>=B-1:
    x = B-1
    ans = floor((A*x)/B) - A*floor(x/B)
else:
    x = N
    ans = floor((A*x)/B) - A*floor(x/B)

print(ans)

E - Rotation Matching

問題のリンク

今回、できなかった問題。テストケース8割は通ったけど、残りがダメでした。

概要

参加者 $N$ 人でジャンケン大会を行う。参加者はそれぞれ $1$ ~ $N$ の番号が割り振られている。
1対1でジャンケンを行う闘技場が $M$ 個用意されている。
闘技場には $N$ 以下の整数が2個割り当てられている。
参加者は自分の数字が書かれた闘技場でジャンケンを行う（第1ラウンド）
その後、参加者に割り振られた整数が1増加する。 $N$ 番目の人は1になる。
参加者は自分の数字が書かれた闘技場でジャンケンを行う（第2ラウンド）
以降、 $N$ ラウンドまで繰り返した時に二回以上同じ参加者と対戦するような参加者が存在しないようにしたい。この時の闘技場の整数はどの様に割り当てるか。

制約

$1 ≤M$
$M × 2 + 1 ≤ N ≤ 100000$

考察

　公式の解説動画が神すぎるくらい分かりやすかったです。最後におまけで出てくるリーグ戦のアルゴリズムも面白かった！

www.youtube.com

2020-04-13

AtCoder ABC 162

AtCoder

ABCD4完の緑パフォでした。以下振り返りと反省。

（2020年4月13日　D問題別解追記）

A - Lucky 7

問題のリンク

概要

3桁の整数 $N$ が与えられる。
$N$ のいずれかの桁に7が含まれるか否か。

制約

$100 ≤ N ≤ 999$
入力は全て整数

考察

特になし

コード

N = input()
if N[0]=='7' or N[1]=='7' or N[2]=='7':
    print('Yes')
else:
    print('No')

B - FizzBuzz Sum

問題のリンク

概要

$1$ から $N$ までの整数で、 $3$ でも $5$ でも割り切れない数を足し合わせる。

制約

$1 ≤ N ≤ 10 ^{6}$

考察

めちゃくちゃFizzBuzzでした。プログラマーなら誰しもが書いてきたもの。

コード

N = int(input())
ans = 0
for i in range(1, N+1):
    if i%3 != 0 and i%5 != 0:
        ans += i

print(ans)

C - Sum of gcd of Tuples (Easy)

問題のリンク

概要

- $\displaystyle{\sum_{a=1}^K}$ $\displaystyle{\sum_{b=1}^K}$ $\displaystyle{\sum_{c=1}^K}$ $gcd(a, b, c)$ を求めよ

制約

$1 ≤ K ≤ 200$

考察

制約を見るからに $a, b, c$ を全てfor文で探索すると[tex: o(N³)]で間に合わなそう。
なので少し工夫をして探索数を減らすことに具体的にはpermutation（順列）ではなく、combinations_with_replacement（重複あり組み合わせ）でgcdを求めて行くことに。それで書いたのが以下のような感じ。

コード

from itertools import combinations_with_replacement

from math import gcd   # gcd(6, 4) -> 2
from functools import reduce

def gcd_list(numbers):
    return reduce(gcd, numbers)


N = int(input())
ans = 0
for i, j, k in combinations_with_replacement(range(1, N+1), 3):
    if i==j==k:
        ans += i
    elif i==j:
        ans += gcd(i, k)*3
    elif j==k:
        ans += gcd(j, i)*3
    elif i==k:
        ans += gcd(i, j)*3
    else:
        ans += gcd_list([i, j, k])*6
print(ans)

学び

ちなみに最初は上のコードのmathをfractionsにして出したところ普通にTLEでした。。。見た感じギリギリっぽかったのと他に良い案が思い浮かばなかったため、mathに変えたところ普通に通りました。。。時間はロスしたものの、手持ちのスニペットが少し整備されたのでそこは良かった。

D - RGB Triplets

問題のリンク

概要

R, G, Bからなる長さ $N$ の文字列 $S$ で、以下の条件を満たす $(i, j, k)$ の組みを求めよ。
$1 ≤ i \lt j \lt k ≤ N$
$S_i ≠ S_j$ かつ $S_j≠ S_k$ かつ $S_k ≠ S_i$
$j-i ≠k-j$

制約

$1 ≤ N ≤ 4000$

考察

これも全探索だと $O(N^3)$ でキツそう
iとjだけの探索なら、 $O(N^2)$ で行けるはず
予め、jの右側にRGBがそれぞれどれだけ存在しているかが分かれば、あとは指定の文字を一々数えなくても自ずと答えはわかる。（累積和を使うことで3つ目のfor文を無くせる。）
例えばi = 'R'、j='G'、であれば、jの左側にどれだけBがいくつ存在するかを見れば良い。
$j-i ≠k-j$ の制約だけ注意。もしこれに該当した場合、上記の値から $-1$

コード

N = int(input())
S = list(input())

num_r = S.count('R')
num_g = S.count('G')
num_b = N - num_r - num_g
C = [[num_r, num_g, num_b] for _ in range(N)]
r_cnt, g_cnt, b_cnt = 0, 0, 0

for i in range(N):
    if S[i] == 'R':
        r_cnt += 1
    elif S[i] == 'G':
        g_cnt += 1
    else:
        b_cnt += 1

    C[i][0] -= r_cnt
    C[i][1] -= g_cnt
    C[i][2] -= b_cnt

ans = 0
for i in range(N-2):
    for j in range(i+1, N-1):
        if S[i] != S[j]:
            if 'R' not in [S[i], S[j]]:
                ans += C[j][0]
                if j+(j-i) < N and S[j+(j-i)]=='R':
                    ans -= 1
            if 'G' not in [S[i], S[j]]:
                ans += C[j][1]
                if j+(j-i) < N and S[j+(j-i)]=='G':
                    ans -= 1
            if 'B' not in [S[i], S[j]]:
                ans += C[j][2]
                if j+(j-i) < N and S[j+(j-i)]=='B':
                    ans -= 1

print(ans)

PyPyで通りました（457ms）。あとで順位表を見てみたところ、このD問題を早く解けるかどうかでだいぶパフォーマンスが違っていたようです。少し実装が複雑になってきたときに素早くバグなく書けるかどうか。。。力の無さを実感します。。。時間出てきたときに後半の問題も追記していきたいと思います。

（2020年4月13日　別解追記） PDF解答をみてなるほどと思ったので、実際にコーディング実装してみました。前のコードに比べるとかなり簡潔に書けてます。ポイントは以下の2点。

$S$ からR G Bの3つのを選ぶ方法はS.count('R') * S.count('G') S.count('B')通り。
制約 $j-i ≠k-j$ を考慮し、この条件に当てはる分を上記の値から引く。iとjをカウンターループさせるので $O(N^2)$

N = int(input())
S = input()

n_R = S.count('R')
n_G = S.count('G')
n_B = N - n_R - n_G
ans = n_R * n_G * n_B

for i in range(N-2):
    for j in range(i+1, N-1):
        k = j + (j-i)
        if k < N:
            if S[i] != S[j] and S[j] != S[k] and S[k] != S[i]:
                ans -= 1

print(ans)

解答見たあとだと、簡単にコーディングもできました。なるほどです。

2020-04-05

AtCoder ABC 161

AtCoder

ABC3完緑パフォでした。以下振り返りと反省。

ABC Swap

問題のリンク

概要

箱 $A, B, C$ に数字 $X, Y, Z$ が入っている。
$A$ と $B$ の中身を入れ替える。
$A$ と $C$ の中身を入れ替える。
最終的な数字の中身は？

制約

$1 ≤ X, Y, Z ≤ 100$
入力は全て整数

考察

勿論一発でprint(Z, X, Y)で行けるし、分かってるんだけど、凡ミスが怖くて謎にダラダラ書きました。（あとで振り返ると逆に間違いやすい気もしなくもない。）

コード

X, Y, Z = map(int, input().split())
X, Y, Z = Y, X, Z
X, Y, Z = Z, Y, X
print(X, Y, Z)

B - Popular Vote

問題のリンク

概要

$N$ 種類の商品について人気投票をした。投票結果は数列 $A$
得票数が $\frac{1}{4M}$ 以上の商品を選べる。
選べる商品数がM以上か否か。

制約

$1 ≤ M ≤ N ≤ 1000$
$1 ≤ A_i≤ 1000$
$A_i$ は異なる
入力は全て整数

考察

普通に全探索した。ちなみにこの問題、出力結果を Yesではなく、YESにしてしまって1WAしてしまいました。C以下の問題で1ペナはきつい。。

コード

N, M = map(int, input().split())
A = list(map(int, input().split()))
to = sum(A)
cnt = 0
for a in A:
    if a>=(to * (1/(4*M))):
        cnt += 1

if cnt >= M:
    print('Yes')
else:
    print('No')

C - Replacing Integer

問題のリンク

概要

整数 $N$ に対して、以下の操作を好きな回数だけ処理できる時、取り得る値の最小値を求めよ。
操作： $x$ を $x$ と $K$ の差の絶対値で置き換える。

制約

$0 ≤ N ≤ 10 ^{18}$
$1 ≤ K ≤ 10 ^{18}$
入力は全て整数

考察

制約を見るからに全探索はできない。
割り切れるだけ割り切った数 $N mod K$ 。もしくはそこから更に $K$ を引いた数が0付近に集まるので、小さくなりそう。

コード

N, K = map(int, input().split())
mod = N%K
print(min(mod, K-mod))

D - Lunlun Number

問題のリンク

概要

隣あうどの2つの桁の値についても、差の絶対値が1以下の数をルンルン数と定義する。
1から数えて $K$ 番目に小さな数を求めよ。

ここはどうやるのか、全然分からず本番中に手も足も出ませんでした。

制約

$0 ≤ K ≤ 10^5$
入力は全て整数

考察

取り敢えず全探索がダメってとこで止まってしまった。
本番後の解説でキューを使うという文言を見て、色々試行錯誤した結果以下のようなコードに、実際に値を取り出してはいないものの、iをイテレータで回していることで、headを1つずつずらしてる。

コード

K = int(input())
Q = list(range(1, 10))
 
for i in range(K):
    x = Q[i]
    y = x%10
    if y != 0:
        Q.append(10*x + y-1)
    Q.append(10*x + y)
    if y != 9:
        Q.append(10*x + y+1)
 
print(Q[K-1])

連続した数字が3つ（もしくは2つ）規則的に出てきてるなってのは実際に数列を手書きしている中で気づいた。
それをキューを使って実装しようという発想が本番中は全く出てこなかった。反省。

E - Yutori

問題のリンク

概要

$N$ 日間のうち、 $K$ 日間働く。
ある日働いたら、その直後の $C$ 日間は働かない。
$S$ のi文字目が x の時は働かない。

解説みて、どう実装すれば良いかはひとまず分かった。でもなぜその様に考えられるかは分かった様な分からない様な感じ。

制約

$1 ≤ N ≤ 2×10^5$
$1 ≤ K ≤ N$
$0 ≤ C ≤ N$
$S$ の長さは $N$
$S$ の各文字はx or o
問題文中の条件を満たすように働く日を選ぶことが可能

方針

スライド作ってみた。 f:id:spider-man-dance:20200405012216p:plain

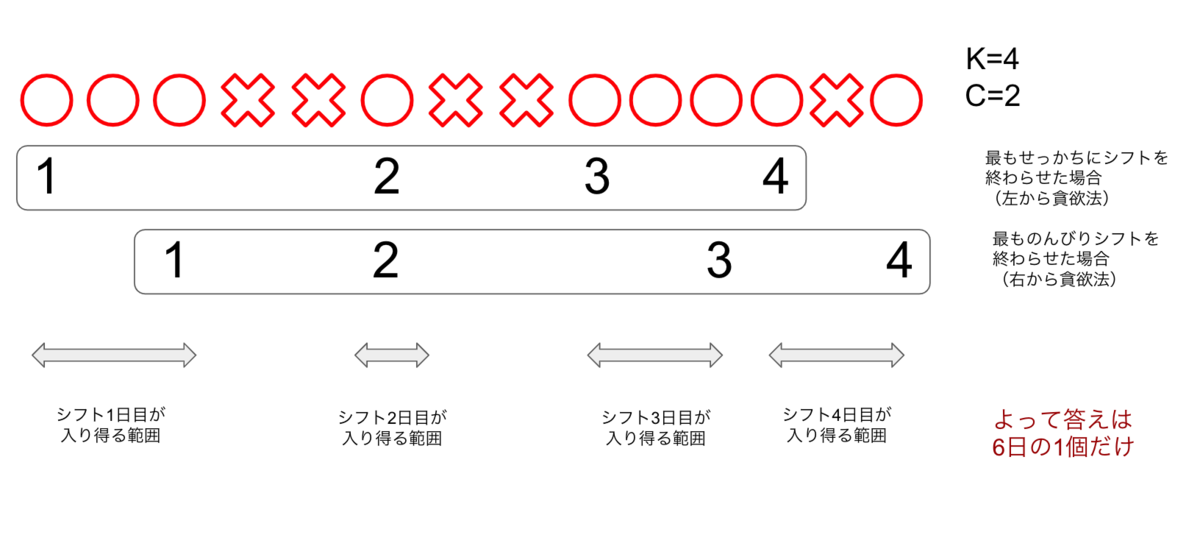
コード

N, K, C = map(int, input().split())
S = list(input())
rS = S[::-1]
lcnt, rcnt = 0, 0
left, right = [0]*N, [0]*N
llimit, rlimit = -1, -1

for i in range(N):
    # 左から貪欲
    # llimit (数字がカウントされた日+C日)以降
    # 上記かつ、シフトに入れる日 ('o')であればシフトに入る。
    if S[i] == 'o' and llimit<i:
        lcnt += 1
        left[i] = lcnt
        llimit = i + C

    # 右から貪欲
    if rS[i] == 'o' and rlimit<i:
        rcnt += 1
        right[-(i + 1)] = K + 1 - rcnt
        rlimit = i + C

#print(left)
#print(right)

# leftとrightで同じ数字が入っている日にちを出力
for i in range(N):
    if left[i]==right[i] and left[i]>0:
        print(i + 1)

2020-03-29

AtCoder ABC 160

AtCoder

　3完でした。DはTLEでしたが、コンテスト終了後にPyPyを選択するとコードの書き換えなしでACでした。。。後の祭りですが、次回からはPythonだけでなく、PyPy試す事忘れずにいきたい。

（2020年4月1日　E問題追記）

A - Coffee

問題のリンク

概要

　文字列の3文字目と4文字目、及び5文字目と6文字目が等しいかどうか。

考察

　特になし

コード

S = input()

if S[2]==S[3] and S[4]==S[5]:
    print('Yes')
else:
    print('No')

B - Golden Coins

問題のリンク

概要

　X円が与えられた時、以下の条件下で喜びを最大化させる。

500円硬貨 1枚につき喜び+1000
5円硬貨 1枚につき喜び+5

制約

$0 ≤ X ≤ 10^9$
$X$ は整数

考察

500円と5円以外は無価値。さらに1円当たりの効果率で言えば、5円玉より500円玉の方が良い。

コード

X = int(input())
n500 = X//500
mod = X%500
n5 = mod//5

print(n500*1000 + n5*5)

C - Traveling Salesman around Lake

問題のリンク

概要

　1週K メートルの湖の周りにN軒の家がある。全ての家を訪れる時の最短距離を求める。

制約

$2 ≤ X ≤ 10^6$
$2 ≤ X ≤ 2×10^5$
$0 ≤ A_1 \lt \cdots \lt A_N \lt K$
入力中のすべての値は整数である。

考察

N軒全ての家を訪れた時点で探索終了ということは、家々の間（家1と家2, 家2と家3, ...）でどれか一つは通らなくても良いということ。であればその中で最も距離が大きいところを除けば、より最短距離で目的が達成できる。

コード

K, N = map(int, input().split())
A = list(map(int, input().split()))

dist = [0] * (N)  # 家々間の距離を初期化
for i in range(N):
    if i != N-1:
        dist[i] = A[i+1] - A[i]  # 家々間の距離を更新
    else:
        dist[i] = K-A[i] + A[0]  # 最初の家とラストの家の間は単純な引き算ではない

print(sum(dist) - max(dist))

D - Line++

問題のリンク

概要

　典型的な最短路問題。制約が結構厳しい。range(N)でループ三回回すとN⁹超える。

制約

$3 ≤ N ≤ 2×10^3$
$1 ≤ X, Y ≤ N$
$X + 1 \lt Y$
入力中のすべての値は整数である。

考察

　最初から最後までダイクストラ法でチャレンジ。

コード1

　Python3では通らず、PyPyでは通るくらい。工夫した点としては、以下の二つ。

中継地点を1 ~ Nまで全て探索するのでなく、バイパスのみに絞る。
上記の処理をするためにSの初期化を工夫（一律Nではない）

from itertools import combinations

N, X, Y = map(int, input().split())

# Sを単純に初期化するのではなく、[2, 1, 0, 1, 2, 3, ...]の様にソートされた状態で初期化
S = [list(reversed(list(range(1, i+1)))) + list(range(N-i)) for i in range(N)]

# バイパスの距離は1
S[X-1][Y-1] = 1
S[Y-1][X-1] = 1

for i in range(N):
    for j in range(N):
        x, y = X-1, Y-1

        # バイパス経由の方が近い場合、距離更新
        S[i][j] = min(S[i][j], S[i][x]+1+S[y][j])

dist = [0]*N
for i, j in combinations(list(range(N)), 2):
    d = S[i][j]
    dist[d] += 1

for i in range(1, len(dist)):
    print(dist[i])

コード2

　終了後に他の人のコードを見て、なるほどと思ったので貼っときます。（ちょっと改変してます）

N, X, Y = map(int, input().split())
ans = [0]*N

for i in range(1, N):
    for j in range(i+1, N+1):
        d = min(j-i, abs(X-i)+abs(Y-j)+1)
        ans[d] += 1

for i in ans[1:]:
    print(i)

　上手いと思ったのは、以下の点

S（二次元配列）を作ってない。そもそもバイパスが存在しなければ、iとjの距離はj-iが保証されているためこの手が使える。
上記に伴って、一度のfor文でans[d] += 1まで処理できてる。自分のコードはS更新後にitertools.combinationsを使ってしまってるので、そこで更に処理時間がかかってしまっている。

E - Red and Green Apples

問題のリンク

コンテスト後にやってみたけど5分くらいで解けた。。。他の人も言っていたけどE問題にしては難易度高くなかったようです。こういうこともあるので、次回のコンテストからは先の問題も目を通していきたい。

概要

赤いリンゴをX。緑のリンゴをY個食べる。
それぞれのリンゴには美味しさ（整数）がある。
美味しさを最大化させるようにリンゴを食べた場合、その最大値を求めることが今回のタスク
色がついてない無色のリンゴも存在し、赤と緑のどちらにも代用可能

制約

$1 ≤ X ≤ A ≤ 10^5$
$1 ≤ Y ≤ B ≤ 10^5$
$1 ≤ C ≤ 10^5$
$1 ≤ p_i ≤ 10^9$
$1 ≤ q_i ≤ 10^9$
$1 ≤ r_i ≤ 10^9$

考察

制約より、無色のリンゴが存在しないと仮定すると、赤いリンゴA個の中から大きい順にX個食べる & 緑のリンゴB個の中から大きい順にY個食べることで、美味しさを最大化することができる。
無色のリンゴはどちらの色にも代用可能であることから、上記でセレクトされたリンゴのうち美味しさの少ないものと無色のリンゴをチェンジしていけば良い。

コード

X, Y, A, B, C = map(int, input().split())
p = sorted(list(map(int, input().split())), reverse=True)
q = sorted(list(map(int, input().split())), reverse=True)
r = sorted(list(map(int, input().split())), reverse=True)

eat_p = p[:X]
eat_q = q[:Y]
eat = sorted(eat_p + eat_q)

for i in range(min(len(eat), len(r))):
    if eat[i] < r[i]:   # 元々のリンゴより無色のリンゴの方が美味しい場合
        eat[i] = r[i]
    else:
        break

print(sum(eat))